Buenas a todos.
Como profesor de matemáticas voy a hablarles sobre las ecuaciones de una variable.
En los siguientes ejercicios obtenga el conjunto de soluciones de la ecuación:
¿Buscas clases de matemáticas online?
Ejercicio 1: 7X + 4 = 25
Solución:
7X + 4 = 25………………………………………………………………………….(1)
La idea es hallar los valores que puede tomar la variable X y que hacen que la ecuación (1) sea verdadera
Ahora se procede a despejar la variable X
El primer paso consiste en agrupar los términos semejantes del mismo lado; por lo tanto, se resta 4 tanto al lado derecho como al lado izquierdo de la ecuación (1) para que se mantenga la igualdad
7X + 4 – 4 = 25 – 4
Ahora se cancelan el +4 y el -4 del lado izquierdo; así mismo, del lado derecho se restan +25 y -4
7X = 21 ……………………………………………………………………………..(2)
El segundo paso consiste en dividir por 7 tanto el lado derecho como el lado izquierdo de la ecuación (2) para que se mantenga la igualdad
7X / 7 = 21 / 7
Ahora en el lado izquierdo se cancelan el 7 del numerador con el 7 del denominador; así mismo, del lado derecho se divide 21 entre 7
X = 3
Por lo tanto, el valor que la variable X puede tomar para que la ecuación (1) sea verdadera es el valor de 3
Comprobación:
7X + 4 = 25
Reemplazando el valor de 3 en la variable X, se tiene
7(3) + 4 = 25
21 + 4 = 25
25 = 25
Del resultado 25 = 25 se puede decir que es una expresión verdadera; por lo tanto, el resultado X = 3 es la solución correcta a la ecuación (1)
Ejercicio 2: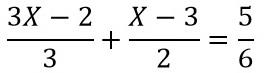 
…...................................................(1)
Solución:
La idea es hallar los valores que puede tomar la variable X y que hacen que la ecuación (1) sea verdadera
Ahora se procede a despejar la variable X
El primer paso consiste en resolver la fracción del lado izquierdo de la ecuación (1) efectuando la suma de las fracciones heterogéneas
Debido a que las fracciones son heterogéneas, se realiza el método de la multiplicación en cruz. De lo anterior se tiene,
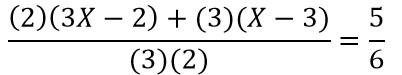...........................................(2)
Se realiza la multiplicación término a término en el numerador y se efectúa la multiplicación del denominador en la ecuación (2)
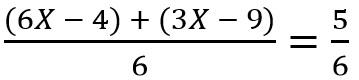............................................................(3)
Ahora se procede a eliminar los paréntesis en la ecuación (3) y se dejan los mismos signos internos porque los paréntesis están precedidos por un signo positivo
....................................................................(4)
Ahora se suman los términos semejantes
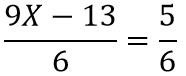....................................................................................(5)
Ahora se procede a multiplicar por 6 ambos lados de la ecuación (5) para eliminar el 6 en el denominador en ambos lados
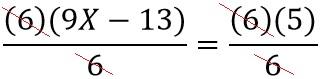........................................................(6)
Simplificando los 6 del numerador y del denominador en la ecuación (6), se tiene
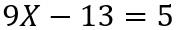.............................................................................(7)
Ahora se procede a sumar 13 en ambos lados de la ecuación (7)
.......................................................................(8)
Cancelando los 13 en el lado izquierdo de la ecuación (8), se tiene
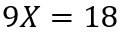.............................................................................................(9)
Ahora se procede a dividir por 9 ambos lados de la ecuación (9)
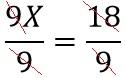.....................................................................(10)
Simplificando en la ecuación (10), se tiene
Por lo tanto, el valor que la variable X puede tomar para que la ecuación (1) sea verdadera es el valor de 2
Comprobación:
.....................................................(1)
Reemplazando el valor de 2 en la variable X de la ecuación (1), se tiene
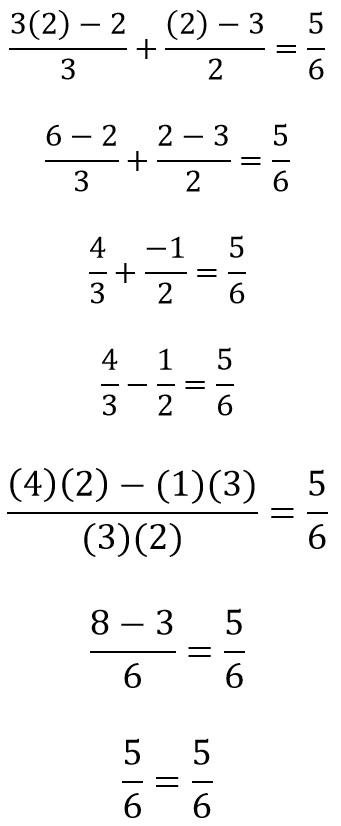
Del resultado 5/6 = 5/6 se puede decir que es una expresión verdadera; por lo tanto, el resultado X = 2 es la solución correcta a la ecuación (1)
Ejercicio 3: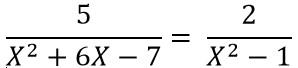 
.................................(1)
Encuentra la solución
Ejercicio 4: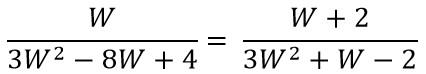 
..............................(1)
Solución:
Encuentra la solución